Soal Teorema Pythagoras dan kunci jawaban serta pembahasannya

****

Berikut ini adalah 10 soal mengenai Teorema Pythagoras yang sudah saya lengkapi dengan kunci jawaban dan pembahasan. Jika ada yang belum paham mengenai perbandingan, silahkan dibaca kembali materi Teorema Pythagoras Part 1 dan Teorema Pythagoras Part 2. 

1. Sebuah segitiga ABC siku-siku di B, dimana AB = 8 cm, AC = 17 cm. Panjang BC adalah ...

a. 9 cm

b. 15 cm

c. 25 cm

d. 68 cm

Pembahasan : 

Diketahui : AB = 8 cm dan AC = 17 cm

perhatikan gambar dibawah ini.

maka, 

AC² = AB² + BC²

17² = 8² + BC²

289 = 64 + BC²

289 - 64 = BC²

225 = BC²

BC = √225 

BC = 15 cm

Jawaban : b

2. Sebuah segitiga siku-siku, hipotenusanya 4√3 cm dan salah satu siku-sikunya 2√2 cm. Panjang sisi siku-siku yang lain adalah ... cm

a. 2√10

b. 3√5

c. 8√2

d. 3√3

Pembahasan :

Diketahui : 

hipotenusanya = 4√3 cm

panjang salah satuh siku-sikunya adalah 2√2 cm

Misalkan, segitiga tersebut adalah segitiga ABC. Maka, perhatikan gambar dibawah ini

sehingga, 

AC² = AB² + BC²

(4√3)² = (2√2)² + BC²

48 = 8 + BC²

48 - 8 = BC²

BC² = 40

BC = √40

BC = √4 X √10 

BC = 2√10 cm

Jawaban : a

3. Jenis segitiga yang dibentuk oleh sisi-sisi 3 cm, 7 cm, dan 8 cm adalah ...

a. segitiga lancip

b. segitiga tumpul

c. segitiga siku-siku

d. segitiga sembarang

Pembahasan : 

Diketahui 

Panjang sisi-sisi 3 cm, 7 cm, dan 8 cm

maka, dengan menggunakan konsep teorema Pythagoras 

c² = a² + b²

8² = 3² + 7²

64 = 9 + 49

64 ≠ 58 >> 64 > 58

Jadi, jenis segitiga yang dibentuk oleh sisi-sisi 3 cm, 7 cm, dan 8 cm adalah segitiga tumpul.

Jawaban : b

4. Panjang BC dari gambar segitiga siku-siku dibawah ini adalah ...

a. 3 cm

b. 6 cm

c. 8 cm

d. 9 cm

Pembahasan : 

Diketahui : 

AC = 12 cm dan AB = 15 cm

maka, 

AB² = AC² + BC²

15² = 12² +  BC²

225 = 144 +  BC²

BC² = 225 - 144

BC² = 81

BC = √81

BC = 9 cm

Jadi, panjang sisi BC adalah 9 cm. 

Jawaban : d

5. Berikut ini adalah ukuran-ukuran sisi-sisi dari 4 buah segitiga. Dari ke 4 buah segitiga tersebut yang terbentuk segitiga siku-siku ditunjukkan oleh nomor ...

a. 1 dan 2

b.  1 dan 3

c. 2 dan 3

d. 1 dan 4

Pembahasan : 

➝ NO. 1 >> 3 cm, 4 cm, 5 cm diperoleh :

c² = a² + b²

5² = 3² + 4²

25 = 9 + 16

25 = 25 ➝ Segitiga siku-siku

➝ NO. 2 >> 7 cm, 8 cm, 9 cm diperoleh :

c² = a² + b²

9² = 7² + 8²

81 = 49 + 64

81 ≠ 113

81 < 113 ➝ Segitiga lancip

➝ NO. 3 >> 5 cm, 12 cm, 15 cm diperoleh :

c² = a² + b²

15² = 5² + 12²

225 = 25 + 144

225 ≠ 169

225 > 169 ➝ Segitiga tumpul

➝ NO. 4 >> 7 cm, 24 cm, 25 cm diperoleh :

c² = a² + b²

25² = 7² + 24²

625 = 49 + 576

625 = 625 ➝ Segitiga siku-siku

Jadi, dari ke 4 buah segitiga tersebut yang terbentuk segitiga siku-siku ditunjukkan oleh nomor 1 dan 4. 

Jawaban : d

6. Diketahui pada gambar berikut, panjang FL = 12 cm dan FM = DE = 16 cm. Maka, keliling dari bangun dibawah ini adalah ...

a. 78 cm

b. 80 cm

c. 86 cm

d. 92 cm

Pembahasan : 

Diketahui :

EK = 20 cm, DE = 16 cm, DF = 8 cm, LM = 20 cm, DM = 8 cm, FL = 12 cm

maka, pertama-tama tentukan terlebih dahulu panjang FK. Karena, segitiga EDK merupakan segitiga siku-siku, sehingga berlaku konsep teorema Pythagoras :

DK² = EK² - DE²

DK² = 20² - 16²

DK² = 400 - 256

DK² = 400 - 256

DK = √144

DK = 12 cm.

Dengan demikian diperolehlah FK = DK - DF ➝ FK = 12 - 8 = 4 cm. 

Jadi, keliling bangun tersebut adalah 

➝ k = EK + DE + LM + DM + FL + FK

➝ k = 20 + 16 + 20 + 8 + 12 + 4

➝ k = 80 cm

Jawaban: b

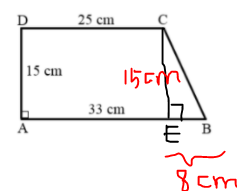
7. Panjang BC dari bangun dibawah ini adalah ...

a. 23 cm

b. 17 cm

c. 16 cm

d. 15 cm

Pembahasan : 

Diketahui : AD = 15 cm, CD = 25 cm, AB = 33 cm

maka, pertama-tama tarik garis CE sebagai berikut. 

Dari gambar diatas panjang CE = AD = 15 cm dan panjang EB = AB - EA = 33 - 25 = 8 cm. 

Sehingga, segita CEB merupakan segitiga siku-siku. 

Dengan menggunakan konsep teorema Pythagoras, diperoleh : 

BC² = EB² + CE²

BC² = 8² + 15²

BC² = 64 + 225

BC = √289

BC = 17 cm. 

Jadi, panjang BC adalah 17 cm. 

Jawaban : b

8. Panjang sisi BC pada gambar dibawah ini adalah ...

a. 16 cm

b. 15 cm

c. 13 cm

d. 12 cm

Pembahasan : 

Diketahui : AB = 9 cm, AD = 17 cm, CD = 8 cm

maka, perhatikan segitiga siku-siku ACD. Panjang AC dapat ditentukan dengan Teorema Pythagoras. 

AC² = AD² - CD²

AC² = 17² - 8²

AC² = 289 - 64

AC² = 225

AC = √225 = 15 cm.

Selanjutnya, perhatikan segitiga siku-siku ABC. Panjang BC dapat ditentukan dengan konsep teorema Pythagoras.

BC² = AC² - AB²

BC² = 15² - 9²

BC² = 225 - 81

BC = √114 = 12 cm. 

Jadi, panjang BC adalah 12 cm. 

Jawaban : d

9. Pada gambar dibawah ini, diketahui bahwa ABCD merupakan jajargenjang dengan panjang CD = 7 cm, AD = 25 cm, dan AE = 22 cm. Sehingga, panjang CE adalah ...

a. 17 cm

b. 20 cm

c. 22 cm

d. 24 cm

Pembahasan : 

Diketahui bahwa AD = BC = 25 cm dan BE = AE - AB = 22- 7 = 15 cm (Perhatikan bahwa AB = CD). Mengapa? Karena, segitiga BEC merupakan siku-siku, maka berlaku konsep teorema Pythagoras, sehingga : 

CE² = BC² - BE²

CE² = 25² - 15²

CE² = 625 - 225

CE = √400 = 20 cm

Jadi, panjang CE adalah 20 cm. 

Jawaban : b

10. Dari tiga bilangan dibawah ini yang merupakan tripel Pythagoras adalah ...

a. 9, 13, 15

b. 7, 12, 15

c. 10, 24, 25

d. 8, 15, 17

Pembahasan : 

➝ Bagian a. 9, 13, 15 

c² = a² + b²

15² = 9² + 13²

225 = 81 + 169

225 ≠ 250 ➝ bukan tripel Pythagoras

➝ Bagian b. 7, 12, 15 

c² = a² + b²

15² = 7² + 12²

225 = 49 + 144

225 ≠ 193 ➝ bukan tripel Pythagoras

➝ Bagian c. 10, 24, 25 

c² = a² + b²

25² = 10² + 24²

625 = 100 + 576

625 ≠ 676 ➝ bukan tripel Pythagoras

➝ Bagian d. 8, 15, 17 

c² = a² + b²

17² = 8² + 15²

289 = 64 + 225

289 = 289 ➝ tripel Pythagoras

Jawaban : d

****

Semoga artikel mengenai Soal Teorema Pythagoras dan Kunci Jawaban serta Pembahasannya bermanfaat dan dapat menambah ilmu kawan-kawan. Jangan lupa selalu berkunjung di blog mathematicsscience yah. 😊😊😊