Barisan dan Deret Geometri : Rumus, contoh soal dan pembahasan lengkap
***
Sebelumnya, blog mathematicsscience telah memberikan artikel tentang Barisan Aritmatika beserta contoh dan pembahasannya lengkap. Selanjutnya, mathematicsscience akan memberikan materi mengenai barisan geometri. Silahkan disimak yah. 😊
BARISAN GEOMETRI
Perhatikan barisan bilangan yang terdiri dari
6. 12, 24, 48, 96, ...
Barisan bilangan di atas memiliki aturan tertentu dalam pembentukannya, dimana suku-suku pada barisan bilangan tersebut dapat diperoleh dari suku sebelumnya, kecuali suku pertama. Perhatikan skema dibawah ini :
atau,
Skema di atas menunjukkan bahwa aturan pembentukan barisan bilangan tersebut adalah "suku setelahnya dibagi dengan suku sebelumnya" atau dapat juga menggunakan aturan "dikali 2". Sehingga, suku-suku berikutnya pada barisan bilangan tersebut adalah 96 x 2 = 192, 192 x 2 = 384, dan seterusnya.
Untuk menentukan rasio atau perbandingan antarsuku yang berurutan pada barisan bilangan tersebut selalu memperoleh hasil yang sama (tetap). Barisan bilangan yang memiliki rasio (perbandingan) antarsuku yang selalu sama seperti barisan bilangan di atas disebut Barisan Geometri.
Dengan demikian, dapat disimpulkan bahwa :
"Barisan geometri adalah barisan bilangan yang mempunyai rasio yang selalu sama (tetap) atau (Un : Un-1) selalu sama. Rasio atau perbandingan antar nilai suku-suku yang berdekatan dilambangkan dengan r. Sedangan suku pertama dilambangkan dengan a".
Bentuk umum dari barisan geometri adalah :
keterangan :
(Un) : suku ke-n
a : suku pertama
r : rasio
DERET GEOMETRI
Deret geometri adalah penjumlahan suku-suku dari barisan geometri. Penjumlahan dari suku-suku pertama sampai suku ke-n barisan geometri dapat ditentukan dengan menggunakan bentuk umum berikut ini :
- dengan syarat r < 1,
- dengan syarat r > 1,
Agar tidak bingung dengan materi yang telah disampaikan di atas, silahkan perhatikan contoh dan pembahasannya berikut ini.
Contoh Soal
1. Selembar kertas dipotong menjadi dua bagian. Setiap bagian dipotong menjadi dua dan seterusnya. Jumlah potongan kertas setelah potongan kelima adalah ...
Pembahasan :
Diketahui :
a = 1
r = 2
n = 5
maka,
(Un) = a x rn
= 1 x 25
= 1 x 25
= 32
Jadi, jumlah potongan kertas setelah potongan kelima adalah 32.
2. Diketahui suatu barisan bilangan yang terdiri dari 3, 9, 27, 81, ... suku ke-6 dari barisan tersebut adalah ...
Pembahasan :
Diketahui :
a = 3
r = 3
n = 6
maka,
= 3 x 36-1
= 3 x 35
= 729.
Jadi, suku ke-6 dari barisan tersebut adalah 729.
3. Jumlah 6 suku pertama dari deret geometri 2 + 6 + 18 + ... adalah ...
Pembahasan :
Diketahui :
a = 2
r = 3
n = 6
maka,
Jadi, jumlah 6 suku pertama pada deret geometri tersebut adalah 728.
Gimana? Apakah kamu sudah paham mengenai materi barisan dan deret geometri di atas? Semoga pembahasan mengenai barisan dan deret geometri lengkap dengan contoh soal dan pembahasannya ini dapat lebih bermanfaat dan menambah catatan sekolah yah.
Terima kasih. 😊😊
***


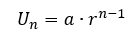

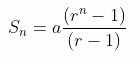



Comments
Post a Comment