Materi dan contoh soal mengenai Barisan dan Deret Aritmatika
***
BARISAN ARITMATIKA
Perhatikan contoh barisan bilangan berikut ini :
6, 9, 12, 15, 18, 21, ...
Pada barisan bilangan diatas memiliki aturan atau pola tertentu dalam pembentukannya, dengan suku-suku pada barisan bilangan tersebut dapat diperoleh dari suku sebelumnya kecuali suku pertama. Aturan Pembentukan barisan bilangan tersebut adalah "ditambah 3". Sehingga, suku-suku berikutnya pada barisan tersebut adalah 21 + 3 = 24, 24 + 3= 27, dan seterusnya.
Untuk menentukan beda antar suku dari barisan aritmatika adalah : U2 - U1 , U3 - U2 , U4 - U3 dan seterusnya selalu memperoleh hasil yang sama. Barisan bilangan yang memiliki beda antarsuku yang selalu sama atau aturan pembentukkannya ditambah bilangan yang sama disebut barisan aritmatika.
Dengan demikian, dapat disimpulkan bahwa :
"Barisan aritmatika adakah barisan bilangan yang mempunyai beda yang selalu sama (tetap) atau (Un - Un-1) selalu sama. Selisih atau beda antara nilai suku-suku yang berdekatan selalu sama yaitu b. Kemudian, nilai suku pertama dilambangkan dengan a".
Bentuk umum dari barisan aritmatika adalah :
keterangan : Un : suku ke-n
a (U1) : suku pertama
b : selisih barisan
DERET ARITMATIKA
Deret arimatika adalah penjumlahan suku-suku dari barisan arimatika. Pejumlahan tersebut dari suku-suku pertama sampai suku ke-n dari barisan aritmatika.
Bentuk umum dari deret aritmatika adalah :
- Jika diketahui suku ke-n :
- Jika diketahui barisan bilangan aritmatika :
Agar tidak membingungkan dengan materi yang telah diberikan, perhatikan contoh-contoh soal beserta pembahasannya berikut ini :
Contoh soal :
1. Diketahui suatu barian bilangan yang terdiri dari 4, 9, 14, 19, ... suku ke-10 dari barisan tersebut adalah ...
Pembahasan :
Diketahui :
a = 4
b = 5
n = 10
maka,
Un = a + (n - 1) x b
= 4 + (10 - 1) x 5
= 4 + 9 x 5
= 4 + 45
U10 = 49
Jadi, suku ke-10 dari barisan tersebut adalah 49.
2. Rumus suku ke-n dari barisan 7, 13, 19, 25, ...
Pembahasan :
Diketahui :
a = 7
b = 6
maka,
Un = a + (n - 1) x b
= 7 + (n - 1) x 6
= 7 + 6n - 6
Un = 6n + 1
Jadi, rumus suku ke-n dari barisan bilangan tersebut adalah 6n + 1.
3. Dalam sebuah gedung pertunjukkan disusun sebuah kursi dengan baris paling depan terdiri dari 10 kursi, baris kedua 12 kursi, baris ketiga berisi 14 kursi dan seterusnya. Banyaknya kursi pada baris ke-10 adalah ...
Pembahasan :
Diketahui :
a = 10
b = 2
n = 10
maka,
Un = a + (n - 1) x b
= 10 + (10 - 1) x 2
= 10 + 9 x 2
= 10 + 18
U10 = 28
Jadi, banyaknya kursi pada baris ke-10 adalah 28.
4. Rumus suku ke-n dari deret bilangan yang terdiri dari 2 + 4 + 6 + 8 + ... + Un adalah ...
Pembahasan :
Diketahui :
a = 2
b = 2
maka,
Bagaimana, sudah paham kan mengenai materi barisan dan deret arimatika?
Semoga pembahasan mengenai barisan dan deret arimatika lengkap dengan contoh soal dan pembahasannya ini bermanfaat dan dapat menambah lagi pengetahun kamu.
Terima kasih.
***


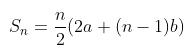



Comments
Post a Comment