20 soal dan pembahasan matematika Kelas 8 smp/mts

 ****

CONTOH SOAL & PEMBAHASAN 

MATEMATIKA SMP/MTS

2020/2021

 

1. Panjang salah satu sisi sebuah persegi panjang adalah 24 cm dan panjang diagonalnya adalah 26 cm. Maka, nilai dari panjang sisi yang belum diketahui adalah ...

Pembahasan :

Diketahui : 

Panjang salah satu sisi sebuah persegi panjang = 24 cm 

Panjang diagonalnya = 26 cm 

maka, perhatikan gambar berikut

c² = a²+ b²  

26² = a²+ 24²

676 = a² + 576

676 - 576 = a²

100 = a² 

a = √100

a = 10 cm. 

Jadi, nilai dari panjang sisi yang belum diketahui adalah 10 cm. 

2. Tiga bilangan asli yang menyatakan panjang sisi-sisi suatu segitiga siku-siku disebut ...

Pembahasan : 

>> Tripel Pythagoras merupakan tiga bilangan asli yang tepat untuk menyatakan panjang sisi-sisi suatu segitiga siku-siku. 

3. Panjang sisi yang sama dari segitiga sama kaki adalah 50 cm. Jika panjang alasnya 96 cm, tinggi segitiga tersebut adalah ...

Pembahasan : 

Diketahui : 

Panjang sisi yang sama dari segitiga sama kaki = 50 cm

Panjang alasnya = 96 cm

maka, perhatikan gambar dibawah ini.

c² = a²+ b²  

50² = a²+ 48²

2.500 = a² + 2.304

2.500 - 2.304 = a²

196 = a²

a = √196

a = 14 cm

Jadi, tinggi segitiga tersebut adalah 14 cm. 

4. Beni akan menyandarkan tangga nya yang panjangnya 20 m pada sebuah tembok. Jarak ujung bawah tangga terhadap tembok 12 m. Maka, tinggi ujung atas tangga dari tanah adalah ...

Pembahasan : 

Diketahui : 

Panjang tangga = 20 m

jarak ujung bawah tangga terhadap tembok = 12 m

maka, perhatikan gambar dibawah ini

c² = a²+ b²  

20² = a²+ 12²

400 = a² + 144

400 - 144 = a²

256 = a²

a = √256

a = 16 cm

Jadi, tinggi ujung atas tangga dari tanah adalah 16 cm. 

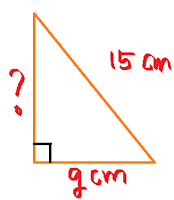
5. Diketahui panjang hipotenusa suatu segitiga siku-siku adalah 15 cm. Jika panjang salah satu sisinya 9 cm, panjang sisi lainnya adalah ...

Pembahasan : 

Diketahui : 

Panjang hipotenusa nya = 15 cm

Panjang salah satu sisinya = 9 cm

maka,perhatikan gambar dibawah ini

c² = a²+ b²  

15² = a²+ 9²

225 = a² + 81

225 - 81 = a²

144 = a²

a = √144

a = 12 cm

Jadi, panjang sisi lainnya adalah 12 cm. 

6. Diketahui sebuah lingkaran mempunyai luas adalah 1.232 cm². Maka, keliling lingkaran tersebut adalah .... cm

Pembahasan :

Diketahui : 

Luas = 1.232 cm²

maka, 

Luas = π・r²

1.232 = 22/7・r²

1.232・7 = 22・r² 

8.624 = 22・r²

r² = 8.624 : 22

r = √392  

r =  19,8 cm. 

sehingga, 

Keliling = 2・ π・r

Keliling = 2・ 3,14・19,8

Keliling = 124,34 cm

Jadi, keliling lingkaran tersebut adalah 124,34 cm.

 

7. Diketahui suatu lingkaran memiliki keliling adalah 22 cm. Maka, jari-jari lingkaran tersebut adalah .... cm 

Pembahasan :

Diketahui : 

Keliling = 22 cm

maka, 

Keliling = 2・ π・r

22 = 2・ π・r

22 : 2 = 22/7・r

11 x 7 = 2・r 

r = 77 : 2 

r = 38,5 cm

Jadi, jari-jari lingkaran tersebut adalah 38,5 cm.

 

8. Diketahui suatu keliling lingkaran adalah 88 cm. Maka luas lingkaran tersebut adalah ... cm²   

Pembahasan :

Diketahui : 

Keliling lingkaran =  88 cm

maka, 

Keliling = 2・ π・r

88 = 2・ 22/7・r

(88 : 2) x 7 = 22・r

308 : 22 = r

r = 14 cm

sehingga, 

Luas = π・r²

Luas = (22/7)・14²

Luas = 616 cm²

Jadi, luas lingkaran tersebut adalah 616 cm²

 

9. Sebuah lapangan berbentuk lingkaran, kelilingnya adalah 1.925 m. Diameter lapangan tersebut adalah .... m 

Pembahasan : 

Diketahui : 

Keliling lingkaran = 1.925 cm

maka, 

Keliling = π・d

1.925 = 22/7・d

d = 1.925 x 7/22

d = 612,5 cm

Jadi, diameter lapangan tersebut adalah 612,5 cm. 

10. Jika diketahui suatu lingkaran AOC mempunyai besar sudut pusat AOC adalah 90 derajat dan panjang OA adalah 14 cm. Maka luas tembereng dari daerah AOC adalah... cm²

Pembahasan : 

Catatan : 

Perlu diingat bahwa cara cepat ini berlaku untuk sudut pusat 90°

Diketahui : r = 14 cm

maka, 

Luas tembereng = (2/7)・r²

Luas tembereng = (2/7)・14²

Luas tembereng = (2/7)・196

Luas tembereng = 56 cm²

Jadi, luas tembereng AOB adalah 56 cm²

 

11. Diketahui besar ∠AOC = 144 derajat dan panjang OC = 42 cm. Maka, luas juring AOC adalah ... 

Pembahasan : 

Diketahui :
∠AOC = 144 derajat

panjang OC = 42 cm

maka, 

luas juring AOC = (144/360)・ π・r²

luas juring AOC = (144/360)・ 22/7・42²

luas juring AOC = 0,4・ 22/7・1.764

luas juring AOC = 2,217.6 cm²

 

12. Diketahui suatu lingkaran mempunyai panjang busur 8,25 cm. Jika panjang diameter dari lingkaran tersebut adalah 21 cm, maka besar sudut pusatnya adalah ... derajat (Л = 22/7) 

Pembahasan :

Diketahui : 

panjang busur 8,25 cm

diameter = 21 cm 

Л = 22/7Л = 22/7maka, Л = 22/7

(∝ / 360) x keliling lingkaran = panjang busur

(∝ : 360) x keliling lingkaran = sudut pusat(∝ : 360) x keliling lingkaran = sudut pusat(∝ / 360) x π x d =  (∝ : 360)8,25

(∝ / 360) x 22/7 x 21 = 8,25

∝ = 45 derajat.

jadi, besar sudut pusatnya adlah 45 derajat. 

13. Unsur-unsur yang merupakan unsur lingkaran adalah...

Pembahasan : 

Unsur-unsur yang merupakan unsur lingkaran adalah jari-jari, Juring, tembereng, apotema, busur, dll.

14. Diketahui dua lingkaran dengan pusat A dan B, jarak AB = 52 cm, jari-jari lingkaran masing-masing 24 cm dan 4 cm. Panjang garis singgung persekutuan luar kedua lingkaran adalah ...

Pembahasan : 

Diketahui : 

Jarak AB = 52 cm

R = 24 cm

r = 4 cm

maka, 

l = √p² - (R - r)²

l = √52² - (24 - 4)²

l = √2.304

l = 48 cm

Jadi, persekutuan luar dua lingkaran tersebut adlah 48 cm. 

 

15. Panjang garis singgung persekutuan dalam dua lingkaran 16 cm. Jika jarak titik pusat kedua lingkaran 34 cm dan panjang jari-jari salah satu lingkaran 20 cm, maka panjang jari-jari lingkaran yang lain adalah ... 

Pembahasan : 

Diketahui : 

d = 16 cm

p = 34 cm

R = 20 cm

maka, 

d = √p² - (R + r)²

(R + r)² =  p² - d²

(20 + r)² =  34² - 16²

(20 + r) = √1.156 -256

20 + r  = 30

r = 10 cm

Jadi, panjang jari-jari yang lainnya adlah 10 cm. 

16. Diketahui dua lingkaran jari-jari lingkaran masing-masing 5 cm dan 3 cm. Jika jarak antara kedua pusat lingkaran adalah 10 cm maka panjang garis singgung persekutuan dalam kedua lingkaran adalah ...

Pembahasan : 

Diketahui : 

R = 5 cm

r = 3 cm

p = 10 cm

maka, 

d = √p² - (R + r)²

d = √10² - (5 + 3)²

d = √100 - 64

d = √36 

d = 6 cm

Jadi, persekutuan dalam dua lingkaran adalah 6 cm. 

 

 17. Diketahui dua lingkaran dengan pusat A dan B, jarak AB = 156 cm, jari-jari lingkaran masing-masing 72 cm dan 12 cm. Panjang garis singgung persekutuan luar kedua lingkaran adalah ...

Pembahasan : 

Diketahui : 

Jarak AB = 156 cm

R = 72 cm

r = 12 cm

maka, 

l = √p² - (R - r)²

l = √156² - (72 - 12)²

l = √20.736

l = 144 cm

Jadi, persekutuan luar dua lingkaran tersebut adlah 144 cm. 

 

18. Diketahui dua lingkaran jari-jari lingkaran masing-masing 15 cm dan 9 cm. Jika jarak antara kedua pusat lingkaran adalah 30 cm maka panjang garis singgung persekutuan dalam kedua lingkaran adalah ...

Pembahasan : 

Diketahui : 

R = 15 cm

r = 9 cm

p = 30 cm

maka, 

d = √p² - (R + r)²

d = √30² - (15 +9)²

d = √900 - 576

d = √324

d = 18 cm

Jadi, persekutuan dalam dua lingkaran adalah 18 cm. 

19. Garis singgung terbagi menjadi 2 yaitu ...

Pembahasan : 

Garis singgung terbagi menjadi 2 yaitu Garis singgung persekutuan luar dua lingkaran dan garis singgung persekutuan dalam dua lingkaran.   

20. Diketahui suatu penampang enam buah kaleng yang berbentuk tabung dengan jari-jari 20 cm. Maka, panjang tali minimal yang diperlukan untuk mengikat enam buah kaleng tersebut adalah ...(Л = 3,14)

Pembahasan : 

Diketahui : 

r = 20 cm

maka, 

p = n・r + 2・ π・r

p = 12・20 + 2・ 3,14・20

p = 365,6 cm