Materi SMP Kelas 8 mengenai pengertian dan bagian-bagian lingkaran

 ****

Lingkaran merupakan salah satu bentuk geometri datar yang banyak ditemui dan dimanfaatkan dalam kehidupan sehari-hari. Lingkaran juga berguna dalam banyak bidang kehidupan sehari-hari, misalnya : olahraga, arsitektur, teknologi, dll. Dalam bidang olahraga, banyak alat olahraga yang memanfaatkan lingkaran seperti pada bentuk lapangan silat, papan target memanah, dan keranjang basket. Pada bidang arsitek, seorang arsitek memanfaatkan bentuk lingkaran pada bentuk yang indah untuk mendekorasi rumah, maupun gedung perkantoran. Seperti bentuk pintu, jendela, maupun atap rumah. Kemudian, pada bidang teknologi bentuk lingkaran juga biasa kita temui, seperti roda mobil, roda motor, setir mobil memanfaatkan bentuk lingkaran. 

A. Mengenal Lingkaran 

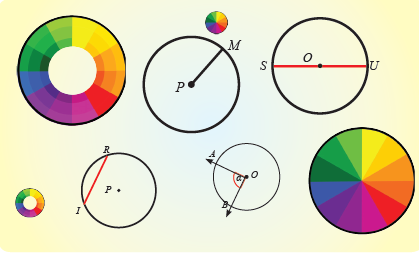
Materi lingkaran sudah pernah dijumpai di Sekolah Dasar (SD). Banyak hal yang akan dipelajari mengenai Lingkaran ini. Perhatikan gambar-gambar dibawah ini yang menunjukkan lingkaran dan bukan lingkaran berikut. 

Dari gambar diatas, dijelaskan bahwa

"Lingkaran merupakan salah satu kurva tutup sederhana yang membagi bidang menjadi dua bagian, yaitu bagian dalam dan bagian luar lingkaran". 

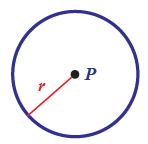
Perhatikan gambar dibawah ini.

Pada gambar diatas, disebut "lingkaran P". Mengapa? Karena, bentuk lingkaran dengan pusat titik P. Jarak yang tetap antara titik pada lingkaran dengan pusat lingkaran dinamakan jar-jari, biasanya disimbolkan dengan r. Selain titik pusat dan jari-jari, masih banyak pula unsur-unsur yang ada pada lingkaran. 

B. Unsur-unsur Lingkaran

Perhatikan gambar dibawah ini. 

Lebih jelasnya, dapat dilihat dibawah ini satu per satu gambar dari Unsur-unsur lingkaran beserta gambarnya sebagai berikut :

1. Titik pusat lingkaran

Titik pusat lingkaran merupakan titik tengah pada suatu lingkaran yang menjadi pusat  lingkaran. 

2. Jari-jari lingkaran

Jari-jari lingkaran merupakan sebuah garis yang menghubungkan antar titik pusat dengan titik lengkung pada keliling lingkaran.

3. Diameter lingkaran

Diameter lingkaran merupakan suatu garis panjang lurus yang menghubungkan dua titik pada keliling lingkaran dan melewati titik pusat lingkaran. 

4. Tali busur lingkaran 

Tali busur lingkaran merupakan garis lurus yang menghubungkan dua titik pada keliling lingkaran. Tetapi tidak melalui titik pusat lingkaran dan berbeda dengan diameter, dimana garisnya melewati titik pusat lingkaran. 

5. Juring lingkaran

Juring lingkaran merupakan suatu luas daerah yang terdapat di dalam lingkaran dan dibatasi oleh dua garis jari-jari dan dibatasi pula oleh sebuah busur lingkaran yang letaknya diapit oleh dua buah jari-jari. 

6. Tembereng lingkaran

Tembereng lingkaran merupakan suatu luas daerah yang berada di dalam lingkaran dan dibatasi oleh busur lingkaran dan tali busur lingkaran. 

7. Apotema lingkaran

Apotema lingkaran merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran. Pada umumnya, garis Apotema ini berada tegak lurus dengan tali busur. 

8. Busur lingkaran

Busur lingkaran merupakan garis lengkung dari keliling lingkaran. Busur pada lingkaran terbagi menjadi 2, yaitu busur besar dan busur kecil. 

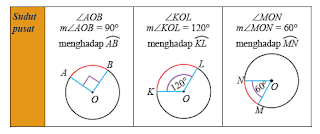
9. Sudut pusat lingkaran

Sudut pusat lingkaran merupakan sebuah sudut yang terbentuk dari perpotongan antara dua buah jari-jari yang terdapat di titik pusat lingkaran. '

10. Sudut keliling lingkaran 

Sudut keliling lingkaran merupakan sebuah sudut yang terbentuk karena adanya pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran. 

B. Menentukan hubungan antara sudut pusat dengan sudut keliling

catatan : 

* Sudut keliling adalah sudut yang kaki sudutnya berhimpit dengan tali busur dan titik pusatnya berhimpit dengan suatu titik pada lingkaran. 

Perhatikan gambar dibawah ini, 

Sudut keliling ABC

Pada gambar diatas, dapat diamati sudut keliling ABC pada lingkaran O. Kaki-kaki sudut ABC memotong lingkaran di titik A dan C. Dengan kata lain sudut keliling ABC menghadap busur AC. Lalu, bagaimanakah hubungan tersebut? 

Sudut keliling dan Sudut Pusat yang Menghadap Busur Sama.

Perhatikan gambar dibawah ini. 

Keterangan : 

simbol "m∠" menyatakan ukuran sudut dan untuk "∠" menyatakan nama sudut. 

Secara umum, dapat disimpulkan bahwa : 

Untuk menghitung sudut pusat dapat menggunakan rumus dibawah ini. 

➝ Sudut pusat = 2 x sudut keliling

* Segiempat Tali Busur

Segiempat tali busur merupakan segiempat yang keempat titik sudutnya berhimpit dengan suatu lingkaran, seperti pada gambar dibawah ini. 

****

Semoga artikel mengenai pengertian dan bagian-bagian lingkaran bermanfaat dan dapat menambah ilmu kawan-kawan. Jangan lupa selalu berkunjung di blog mathematicsscience yah. 😊😊😊