Pertidaksamaan Linear Satu Variabel _ SMP Kelas 7
Perhatikan contoh berikut ini.
- a). 3 < 2 + 4
- b). 4 + 5 > 7
- c). 3 + x ≤ 8
- d). 5x + 2 ≠ 11
- e). 2 ≥ 1
Diantara contoh - contoh a hingga e terdapat lambang ketidaksamaan. Tetapi, untuk kalimat a, b dan e dikatakan "ketidaksamaan" sedangkan kalimat c dan d dikatakan "pertidaksamaan". Mengapa demikian? Karena, dapat disimpulkan bahwa :
- Ketidaksamaan adalah kalimat yang menggunakan tanda ketidaksamaan.
- Pertidaksamaan adalah kalimat terbuka yang menggunakan tanda ketidaksamaan dan mengandung variabel.
Berikut ini lambang ketidaksamaan beserta artinya :
2. Pengertian pertidaksamaan linear satu variabel
- Konsep pertidaksamaan linear saru variabel
Misalkan a dan b adalah bilangan riil, a ≠ 0. Pertidaksamaan linear dapat dinyatakan dalam bentuk :
- ax + b > 0
- ax + b < 0
- ax + b ≤ 0
- ax + b ≥ 0
Perhatikan contoh berikut ini.
- x > 5
- y + 4 < 14
- p ≥ 15
Pada contoh diatas terlihat bahwa, pertidaksamaan a, b dan c mempunyai satu variabel dengan pangkat tertinggi dari variabel tersebut adalah 1. Sehingga, dapat disimpulkan bahwa :
"Pertidaksamaan linear satu variabel (PtLSV) adalah pertidaksamaan yang hanya memiliki satu variabel dengan pangkat tertinggi dari variabel tersebut adalah 1".
3. Sifat-sifat pertidaksamaan
- Jika kedua ruas pertidaksamaan ditambah atau dikurang dengan sebuah bilangan maka tanda pertidaksamaan tetap.
- Jika kedua ruas pertidaksamaan dikali ataupun dibagi dengan suatu bilangan positif maka tanda pertidaksamaannya tetap.
- Sedangkan, jika kedua ruas pertidaksamaan dikali ataupun dibagi dengan suatu bilangan negatif maka tanda pertidaksamaannya berubah.
contoh :
Tentukan penyelesaian dari pertidaksamaan 3x + 6 > 2x - 5!
Penyelesaian :
3x + 6 < 2x - 5
3x - 2x < -5 - 6
x < - 11
x > -11
4. Menyelesaikan pertidaksamaan linear satu variabel (PtLSV)
Bagaimana cara kita menyelesaiakan suatu pertidaksamaan linear satu variabel? Untuk menyelesaikan suatu pertidaksamaan linear satu variabel dapat dilakukan dengan 2 cara, yaitu :
- Menentukan terlebih dahulu penyelesaian persamaan yang diperoleh dari pertidaksamaan dengan cara mengganti tanda ketidaksamaan dengan tanda sama dengan.
- Menyatakannya ke dalam pertidaksamaan yang setara (ekuivalen).
Contoh :
1. Tentukan penyelesaian pertidaksamaan berikut, untuk variabel x adalah bilangan bulat positif.
- a). 7x > 21
- b). 2(x - 4) ≥ 8
- c). 3(4x - 10) < 6
- d). 10x + 3 ≤ 5x + 38
Penyelesaian :
a). 7x > 21
maka,
dengan, x = {4, 5, 6, 7, ... }.
b). 2(x - 4) ≥ 8
maka,
dengan, x = {1, 2}d). 10x + 3 ≤ 5x + 38
maka,
dengan, x = {1, 2, 3, 4, 5, 6, 7}`
2. Tentukan himpunan penyelesaian masing-masing pertidaksamaan berikut untuk variabel x adalah bilangan riil.
- a). -(2x + 6) + 8 < 2(2x - 5)
- b). 2x - (5x - (6x + 2)) > 10 - x
Penyelesaian :
a). -(2x + 6) + 8 < 2(2x - 5)
maka,
dengan, x = {3, 4, 5, ... }
b). 2x - (5x - (6x + 2)) > 10 - x
maka,
dengan, x = {3, 4, 5, ...}
3. Sebuah bus pariwisata berisikan 50 anak. Jumlah anak laki-laki di dalam bus itu adalah 4 orang lebih sedikit daripada anak perempuan.
- a). Nyatakan permasalahan tersebut dalam kalimat matematika.
- b). Tentukan jumlah anak laki-laki dalam bus tersebut.
- c). Tentukan jumlah anak perempuan dalam bus tersebut.
Penyelesaian :
Misalkan,
- x = anak laki-laki
- y = anak perempuan
a). maka, y = x + 4
dengan, catatan bahwa x < y, dimana y = x + 4
sehingga,
>> x + y = 50
>> x + x + 4 = 50
>> 2x = 50 - 4
>> 2x = 46
>> x = 23 orang
b). Jadi, jumlah anak laki-laki dalam bus tersebut adalah 23 orang.
c) Jadi, jumlah anak perempuan dalam bus tersebut adalah 27 orang.
>> y = x + 4
>> y = 23 + 4
>> y = 27 orang
4. Syarif mendapatkan nilai ujian matematika 84, 96, 80 dan 93 pada empat ujian yang pertama. Tentukan nilai ujian terkecil yang harus diraih Syarif pada ujian kelima agar ia memperoleh rata-rata paling sedikit 90.
Penyelesaian :
Diketahui rata-rata nilai ujian Syarif = 84, 96, 80 dan 93
maka,
sehingga, untuk nilai ujian ke 5, Syarif harus memperoleh nilai :
Semoga bermanfaat.
Terima kasih.



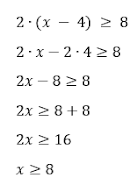


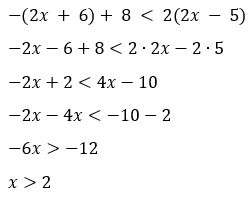
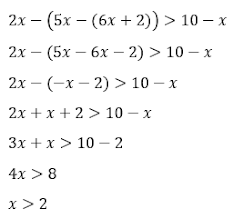




Comments
Post a Comment